目录
梁端无隔板支撑桥面板有效工作宽度计算
陈维晃 2025.03.15
板在局部分布荷载$p$的作用下,不仅直接承压部分(例如宽度为 $a_2$)的板带参加工作,与其相邻的部分板带也会分担一部分荷载共同参与工作。因此,在桥面板的计算中,就有一个如何确定板的有效工作宽度的问题。
1.桥面板有效工作宽度
现在考察一块跨径为 $l$,宽度较大的梁式行车道板的受力状态。当荷载以 $a_2 × b_2$ ,的分布面积作用在板上时,板除了沿计算跨径 $x$方向产生挠曲变形 $w$外,在沿垂直于计算跨径的 $y$方向也必然发生挠曲变形 $w_y$。这说明荷载作用下,不仅承压宽度为 $a_2$的板条直接受力,而且邻近的板也参与工作,共同承受车轮荷载所产生的弯矩。
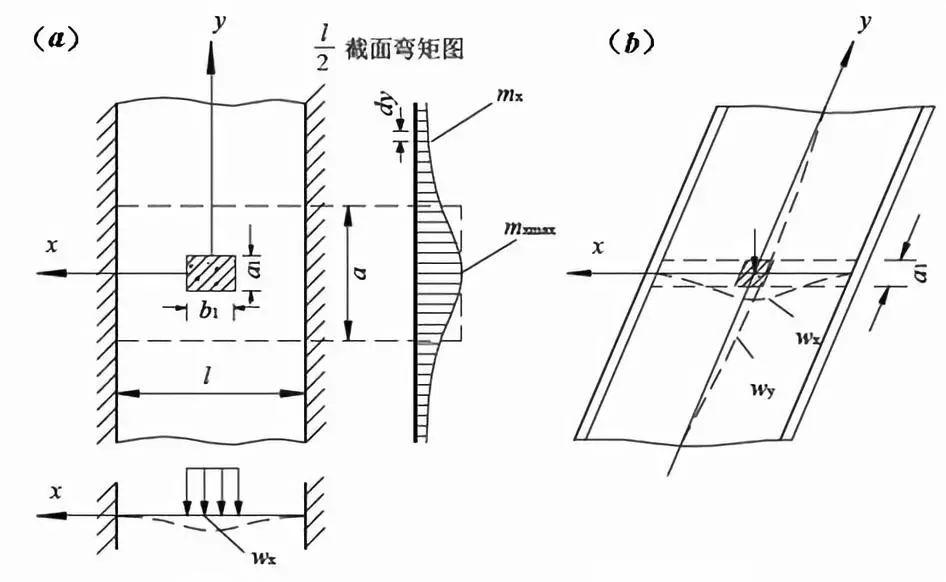
由图可见,跨中弯矩 $m_x$ 的实际图形是呈曲线分布的,在荷载中心处达到最大值,离荷载愈远的板条所承受的弯矩愈小。
如果设想以 $a×m_{xmax}$的矩形来替代此曲线图形,即
$$ a×m_{xmax} = \int m_x dy = M $$
则得弯矩图形的换算宽度为:
$$ a = \frac{M}{m_{xmax}} $$
以上内容来自周水兴老师的《桥梁工程(第2版)》第5章 混土简支梁桥。
2.梁端桥面板类型
2.1全高度横隔板T梁
对于装配式T梁等结构,教科书中的算法,针对的是跨中远离隔板位置的计算,对于跨中接近隔板位置的桥面板以及梁端桥面板,因为隔板对桥面板的支撑作用,实际内力将比前者小很多,故一般不做计算。
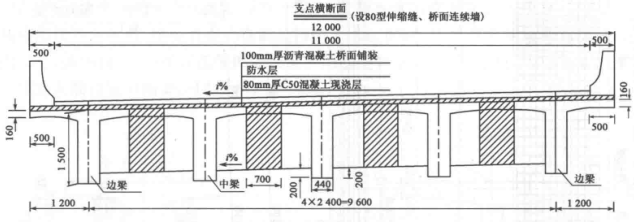
2.2部分高度横隔板T梁
横隔板在施工过程中存在脱模困难等问题,部分设计院创新性的提出了部分高度横隔板T梁。如下图所示:
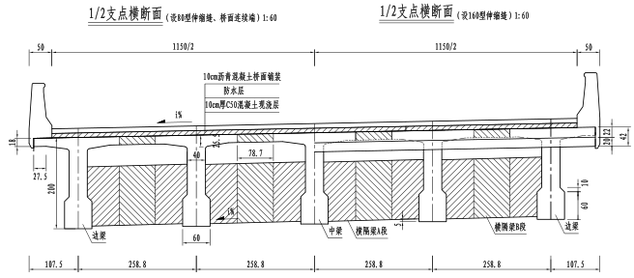
该类T梁在设80伸缩缝以及桥面连续的端头位置的桥面板,因缺少隔板支撑,顺桥向受力类似于悬臂梁,《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG 3362-2018)》以及教科书上对于板的有效工作宽度的算法并不完全适用。
3.梁端桥面板有效工作宽度计算
3.1国外规范的规定参考
日本组合梁规范中对于梁端桥面板的规定如下:

翻译如下:
与一般截面相比,主梁梁端的桥面板受到的弯矩更大,因为该位置的结构连续性被打断。根据有限元法的分析结果,梁端面板横桥向方向上的弯矩约为一般截面的2倍。另外,安装伸缩缝的梁端位置,由于结构不平整,车辆荷载很容易直接作用在主梁梁端的桥板上。因此,最好用足够刚性的端支架支撑主梁端部的桥面板,因为与其他截面相比,梁端更容易损坏。
3.2有限元法计算梁端有效工作宽度
本节以一个宽度$2.6m$,长度$30.0m$,板厚$18cm$简支板为例,分别在跨中和梁端施加一个车轮荷载,根据车轮荷载效应分析桥面板梁端有效工作宽度。
根据《公路桥涵通用设计规范(JTG D60-2015)》表4.3.1-3 车辆荷载的主要技术指标,中、后轮着地宽度及长度为$60×20cm$,后轴重力标准值为$2×140kN$,单个车轮竖向力标准值为$70kN$。桥面铺装厚度按常规装配式T梁做法,取$10cm$沥青混凝土+$10cm$混凝土现浇层。
3.2.1荷载集度计算
车轮荷载作用在跨中桥面板,荷载扩散后的均布荷载集度为:
$$P=\frac{70kN}{1.0m × 0.6m}=116.6kN/m^2$$
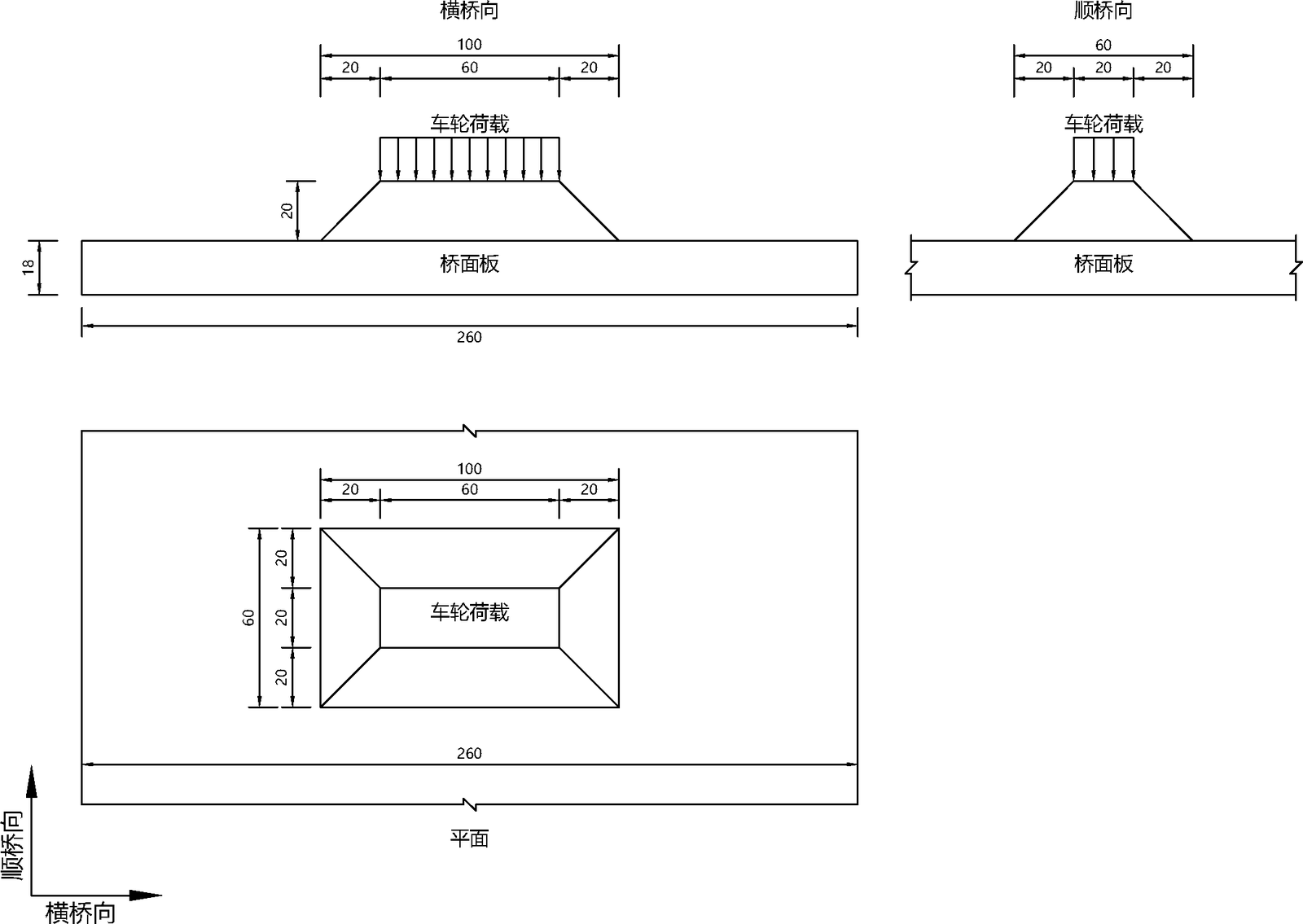
车轮荷载作用在梁端桥面板,荷载扩散后的均布荷载集度为:
$$P=\frac{70kN}{1.0m × 0.4m}=175.0kN/m^2$$

3.2.2有限元分析结果
建立两个$2.6m×30.0m$的有限元模型(为便于显示,此处对模型旋转$90°$显示)。
在模型1跨中施加面积为$1.0m×0.6m$,集度为$116.6kN/m^2$均布荷载;
在模型2跨中施加面积为$1.0m×0.4m$,集度为$175.0kN/m^2$均布荷载。
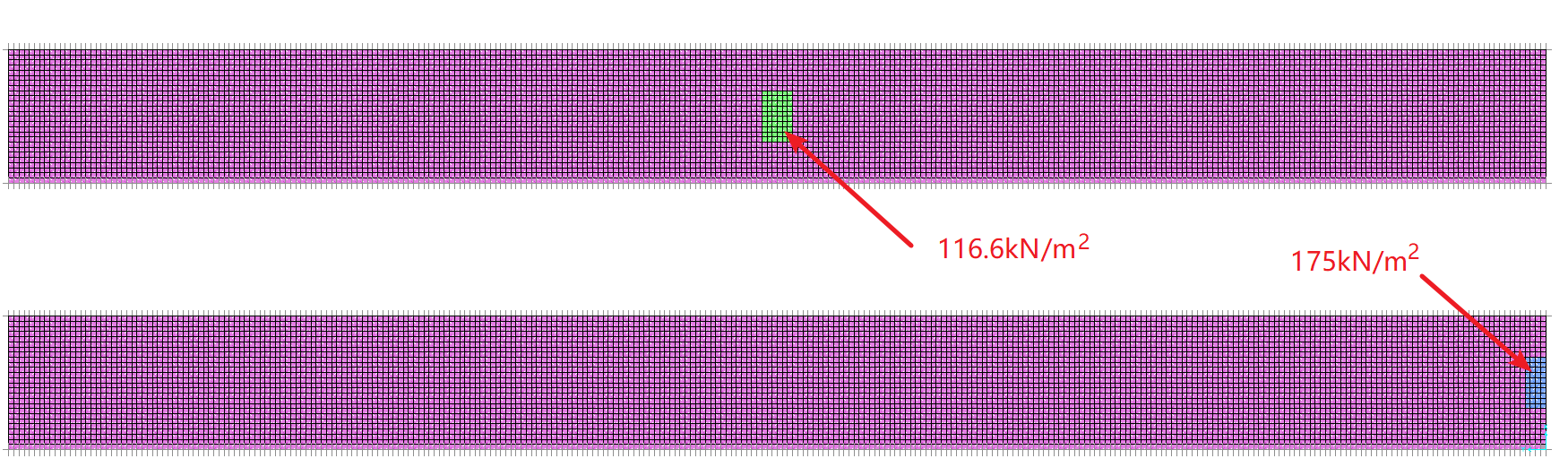
横桥向(2.6m方向)弯矩云图如下:

横桥向跨中位置,沿顺桥向进行截面剖腹,提取弯矩分布图,结果如下:


模型2相比模型1,因为集度更大作用面积更小,弯矩峰值也远大于模型1。因为作用的荷载均为一个车轮荷载,两个模型的弯矩分布图积分后的图形面积(合力弯矩)也将一致。故这里假设面积为$M$,不进行积分计算。
提取两个模型的弯矩峰值如下:
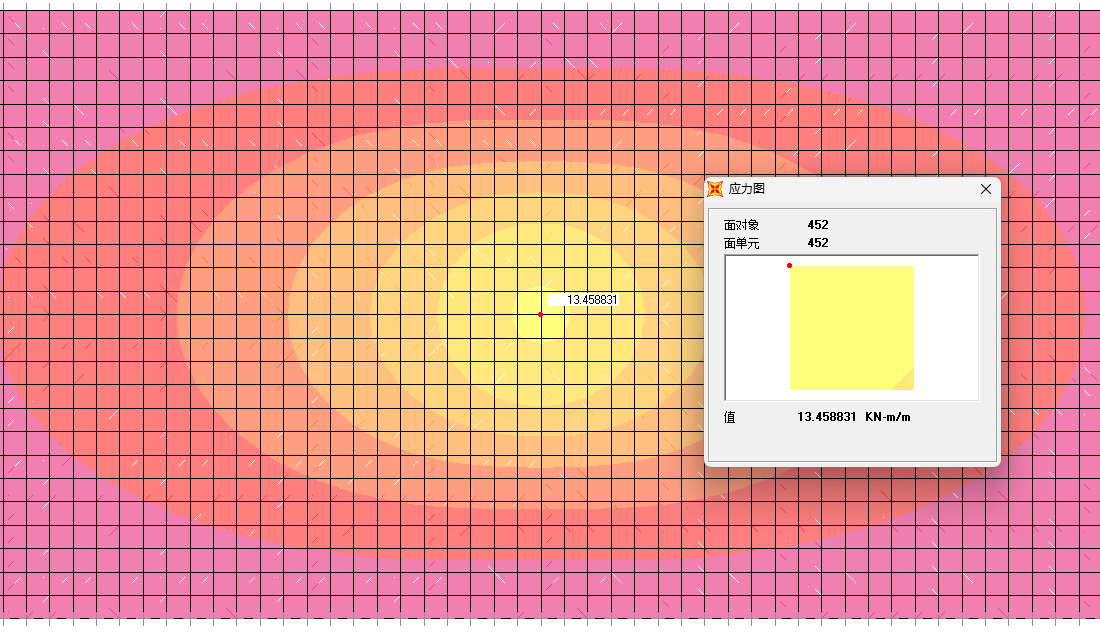
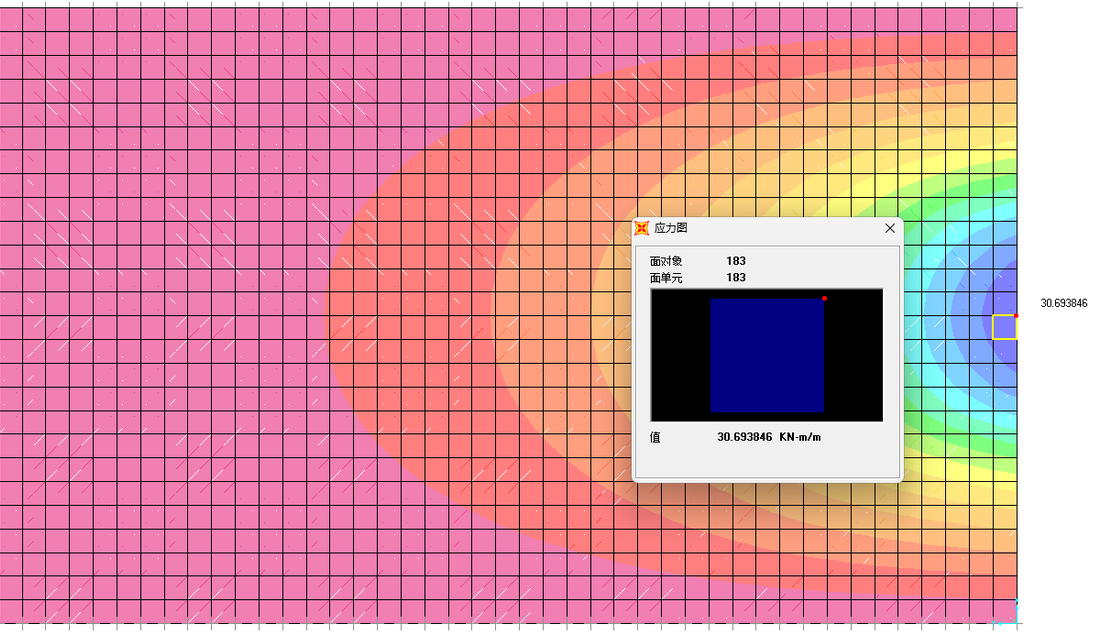
根据换算宽度计算公式可得,跨中有效工作宽度表达式为:
$$ a_m = \frac{M}{13.459} $$
跨中有效工作宽度表达式为:
$$ a_e = \frac{M}{30.694} $$
可得,跨中与梁端的有效工作宽度之比为:
$$ \frac{a_m}{a_e} = \frac{\frac{M}{13.459}}{\frac{M}{30.694}}=\frac{30.694}{13.459}=2.28 $$